题解 P4305 【[JLOI2011]不重复数字】

发表于 | 更新于 | 阅读次数：
本文字数： 2.1k | 阅读时长 ≈ 2 分钟

前言

题解中的各位神仙的$hash$、$map$、重载运算符等等的花里胡哨的东西，我看都看不懂,然后就自闭了，但其实这道题并不用这样写。

一个好习惯

不管是考试还是自己刷题，先看一下数据范围

对于$100\%$的数据，$1 <= N <= 50000 $，给出的数在$ 32 $位有符号整数范围内。$ T≤50 $

算一下，$N*T=2500000，$这不是随便跑吗，于是，我就开始入手 桶排$+$暴力。

介绍一下桶排

桶排序 $(Bucket sort)$或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间$（O（n））$。但桶排序并不是 比较排序，他不受到 $O(nlog_n)$ 下限的影响。

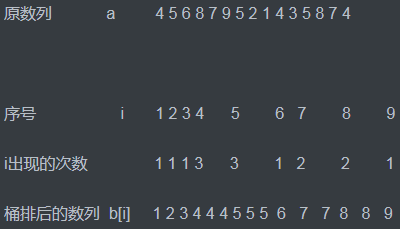
对于上图，$a$是原数列，在$a$的最大值是$9$,我们就开$9$个桶，第$i$的桶记录的是$i$在$a$中出现的次数，最后直接输出就好了。

但桶排并不是万能的，比如说下面这样一个数列$：”1,1,1,1,1,1,1,1,1,1,…,1,1e^9”$,中间有很多个$1$,最后一个$1e^9$，那这样按照桶排的方法的话，我们要开一个$1e^9$的桶，那就$MLE$了，这个时候就需要另一种排序方式了

基数排序

基数排序$（radix sort）$属于“分配式排序”$（distribution sort）$，又称“桶子法”$（bucket sort）$或$bin sort$，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为$O (nlog_r m)$，其中$r$为所采取的基数，而$m$为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

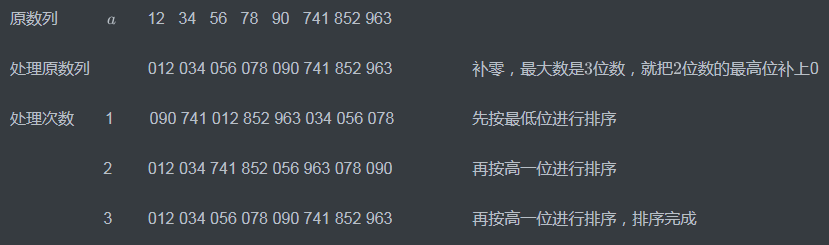
$P.S.$在排序时，本次处理必须和上次处理是稳定排序

稳定排序是什么呢？

稳定排序

待排序的记录序列中可能存在两个或两个以上关键字相等的记录。排序前的序列中$R_i$领先于$R_j$（即$i<j$）.若在排序后的序列中$R_i$仍然领先于$R_j$，则称所用的方法是稳定的。

即

处理次数$2$时有$”012”和”852”$这两个数，但由于在处理次数$1$时$”012”$在$”852”$的前面，所以基于稳定排序，在处理次数$2$时要把$”012”$放在$”852”$的前面，否则这就是不稳定排序。

关于这道题

由于数据范围较小，所以我们可以桶排去写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll long long

using namespace std;

const ll FFF=5e5+5;

ll t,n;
ll a[FFF],b[FFF];//a数组是原数组，b数组是桶数组
bool flag[FFF];//flag记录该数是否输出过

int main()
{
	//if(fopen(".in", "r"))
	//{
	//	freopen(".in", "r", stdin);
	//	freopen(".out", "w", stdout);
	//}
	ios::sync_with_stdio(false);
	cin>>t;
	for(int j=0;j<t;++j)
	{
		memset(flag,1,sizeof(flag));//初始化flag，1表示尚未输出，0表示已经输出
		cin>>n;
		for(int i=1;i<=n;++i)
		{
			cin>>a[i];//输入原数组
			b[a[i]]+=1;//并将原数组载入桶数组
		}
		for(int i=1;i<=n;++i)
		{
			if(b[a[i]]==1)//如果这个数只出现了一次
			{
				cout<<a[i]<<" ";//就直接输出
         	 }
			else//否则就需要去重操作
			{
				if(flag[a[i]]!=0)//如果这个数尚未输出
				{
					cout<<a[i]<<" ";//就输出一遍
					flag[a[i]]=0;//并把flag即为0，表示已经输出过了
				}
			}
		}
		cout<<endl;//在两次询问之间要有换行
	}
	return 0;
}