暴力
当看到$n≤2500$和5000ms/512MB的时空限制时,
我就想到 开花 暴力(看到iki9奆佬的暴力之后,我深深地感受到了我是多么地菜)
这道题的暴力其实比较好打,按着题意打就可以了,
我的是 $ O(n^3) $ 暴力,所以我的暴力这道题并过不去,那我打出来干什么呢?仅供欣赏,不做讲解(同样打 $ O(n^3) $ 暴力的同学可以去这里交一下,题目有一点小魔改,需要改一下程序的)
1 |
|
应该是正解吧
我们看一下本题的三个条件
- 对于每一个$i,j,a_{i,j}=a_{j,i}$(在矩阵中就是左下角的数和右上角的数对称相等)
- 对于每一个$i,a_{i,i}=0$(在矩阵中就是对角线都为 0)
- 对于每一个$i,j,k,a_{i,j}≥max(a_{i,k},a_{k,j})$(在矩阵中就是对于任意一个格子$(i,j)$要满足对于任意的 $k$,$a_{i,j}≥max(a_{i,k},a_{k,j})$,k 为$1$~$n$中的任意数,可以与$i,j$相等)
是不是看起来有一点眼熟?
- $a_{i,j}=a_{j,i}$,表示无向图
- $a_{i,i}=0$,表示无自环
- $a_{i,j}≥max(a_{i,k},a_{k,j})$,表示最小生成树
所以,这道题可以用最小生成树去写。
复杂度$O(n^2)$,可以$*$过此题
具体写法
第一个和第二个条件直接$O(n^2)$判断过去就好了,不表
我们重点讲然如何判断第三个条件(敲黑板)
怎么判断这个矩阵是不是最小生成树呢?
我们先把它看做一个邻接矩阵,
建立一个完全图,
如果这个图是的任一个生成树都是最小生成树的话,
则满足题意,输出“MAGIC”。
那么重点在于如何去证明这个完全图的任一个生成树都是最小生成树。
我们可以看一下下面的图
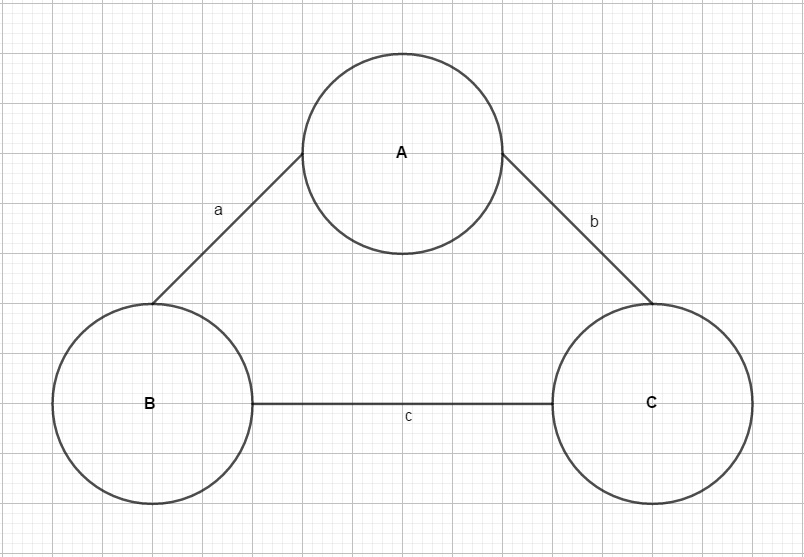
如果$max(a,b)≤c$,那么如果按照最小生成树的方法,应该选择连接$B-A-C$才是正确的连法,
否则这个完全图就不满足题意了。
下面是判断第三个条件的代码
1 | for(int i=0;i<n;++i) |
献上我丑陋的AC代码
1 |
|