题解 P3367 【【模板】并查集】

前言

这道题是一道对初学者有点不太友好的题目，因为一开始可能有点难理解（理解之后可能还好），可是这道题又是一道初学者必须码的一道题（比如说我这种蒟蒻）

---

题意

我们先理解一下题意，题目提供了两个正整数$n$，$m$,表示有$n$个元素，$m$次询问。接着他给了你$m$行询问，一行询问有$z$,$x$,$y$三个数。当$z$=1时，将$x$与$y$所在的集合合并;当$z$=2时，输出$x$与$y$是否在同一集合内，是的话输出$Y$；否则话输出$N$。

---

核心模板

1. 找爸爸

   $f[x]$是指$x$的爸爸（P.S. 一开始每个元素的爸爸就是它自己）

   int find(int x)
      {
      	if(f[x]==x)//如果一个元素的爸爸就是它自己
      	{
      		return x;//就直接返回它自身
      	}
      	else
      	{
      		f[x]=find(f[x]);//否则就接下去寻找，直到找到他的爸爸为止
      	}
      	return f[x];//返回它的爸爸的值
      }

2. 合并（就是当z=1时）

   void work1(int x,int y)
      {
      	f[find(y)]=find(x);
      }

   合并的本质就是使$x$和$y$的爸爸变成同一个爸爸（逃
   $find(x)$是找到$x$的爸爸，$f[find(y)]$是找到$y$爸爸的爸爸（它的祖先？雾。。。）并使他们相等，也就是让$x$和$y$的集合合并。
   原理见图：
   
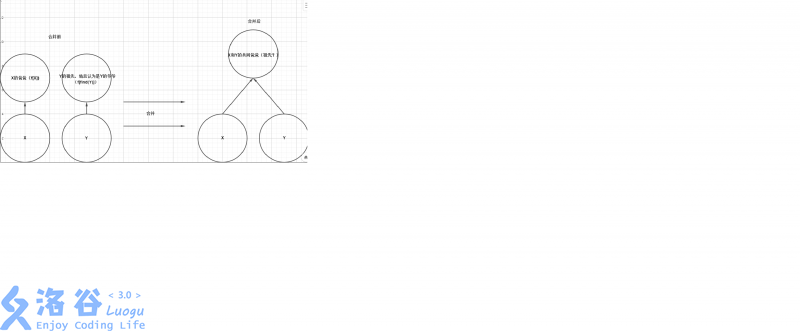
   从图中可以看出，合并之后$x$和$y$就成为了兄弟，也就是在同一个集合内了（集合合并）

3. 查询（也就是当z=2的时候）

void work2(int x,int y)//查询
    {
    	if(find(x)==find(y))//查询是否为同一个爸爸
    	{
    		cout<<"Y"<<endl;//是就输出“Y”
    	}
    	else
    	{
    		cout<<"N"<<endl;//不是就输出“N”
    	}
    }

如果$x$和$y$的爸爸是同一个的话，那么$x$和$y$就是兄弟，也就是说$x$和$y$在同一集合中，所以输出$Y$，不然就输出$N$。

---

把以上模板拼接一下，就是AC代码啦

#pragma GCC optimize(3)//O3优化不用管啦
#include<bits/stdc++.h>
using namespace std;
int n,m,z[666666],x[666666],y[666666];
int f[666666];
int find(int x)//找爸爸 
{
    if(f[x]==x)
    {
        return x;
    }
    else
    {
        f[x]=find(f[x]);
    }
    return f[x];
}
void work1(int x,int y)//合并
{
    f[find(y)]=find(x);
}
void work2(int x,int y)//查询
{
    if(find(x)==find(y))
    {
        cout<<"Y"<<endl;
    }
    else
    {
        cout<<"N"<<endl;
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    ios::sync_with_stdio(false);//关闭同步使cin，cout变快
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>z[i]>>x[i]>>y[i];
        f[i]=i;
    }
    for(int i=1;i<=m;i++)
    {
        if(z[i]==1)
        {
            work1(x[i],y[i]);
        }
        else
        {
            work2(x[i],y[i]);
        }
    }
    return 0;//完结撒花
}